Define Second Order Differential Equation

By Un_389Tatiana 27 Aug, 2022 Post a Comment

Examples of Second Order Reactions. Partial Differential Equation Toolbox provides functions for solving structural mechanics.

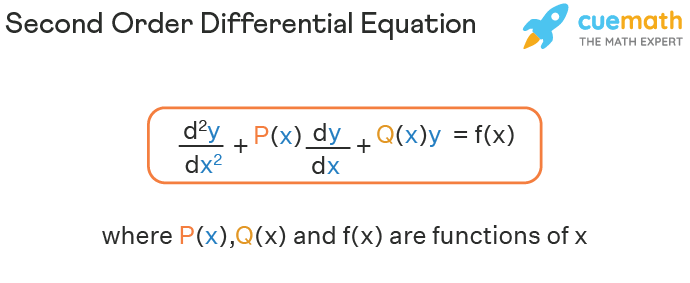
Second Order Differential Equation Solver Types Examples Methods

An ordinary differential equation ODE is an equation containing an unknown function of one real or complex variable x its derivatives and some given functions of xThe unknown function is generally represented by a variable often denoted y which therefore depends on xThus x is often called the independent variable of the equation.

. For example the amount of bunnies in the future isnt dependent on the number of bunnies right now because it takes a non-zero amount of time for a parent to come to term after. Well not actually be solving this at any point but since we gave the higher dimensional version of the heat equation in which we will solve a special case well give this as well. Learn more about first order differential equations here.

Since second order reactions can be of the two types described above the rate of these reactions can be generalized as follows. This also represents a First order Differential Equation. Generate mesh define physics with load boundary and initial conditions solve and visualize results all from one.

This shows a relationship between the second derivative of y with respect to x AND a term that depends on y and one that depends. Methods of resolution The table below summarizes the general tricks to apply when the ODE has the following classic forms. The 2-D and 3-D version of the wave equation is.

When the order of the highest derivative present is 2 then it is a second order differential equation. A few examples of second order reactions are given below. For the sake of completeness well close out this section with the 2-D and 3-D version of the wave equation.

So for the heat equation weve got a first order time derivative and so well need one initial condition and a second order spatial derivative and so well need two boundary conditions. Second Order Differential Equation. Inverted Spring System Example.

The solutions to this equation define the Bessel functions and The equation has a regular singularity at 0 and an irregular singularity at. R kA x B y. If you are not familiar with this kind of conversion refer to Differential Equation meeting Matrix Example.

Where the sum of x and y which corresponds to the order of the chemical reaction in question equals two. There are many additional features you can add to the structure of a differential equation. A transformed version of the Bessel differential equation given by Bowman 1958 is.

Ordinary differential equations are only one kind of differential equation. Now we have a differential equation that is a bit more complicated. The term ordinary is used in contrast.

Inverted Spring-Mass with Damping. Once you have a set of differential equation which are all first order you can easily convert it in the form of Matrix equation as shown below. In partial differential equations the same idea holds except now we have to pay attention to the variable were differentiating with respect to as well.

Solve second-order linear and nonlinear PDEs for stationary time-dependent and eigenvalue problems.

Second Order Linear Differential Equations Youtube